Letter in Physical Review B
In an earlier blog post we discussed how neutrons – a work-horse probe of condensed matter – may give deeper access to quantum many-body states than previously realised. At the heart of that work was the idea that the static structure factor (what neutron scattering measures) can, in favourable cases, uniquely determine the quantum wave-function or at least the ground state of a quantum magnet. We are now excited to report our new paper,
“Fitness landscape for quantum state tomography from neutron scattering”
(T. Tula, J. Quintanilla & G. Möller, Phys. Rev. B 112, L140402 (2025), DOI 10.1103/x9mb-x1gz),
which has just been published as a Letter and takes this idea further — moving from the theoretical existence of a relation between scattering data and the quantum state, towards exploring how easy or hard it is in practice to invert scattering data into state information.
In short: we’ve begun mapping out the “fitness landscape” for quantum-state tomography from neutron scattering data.
What the new work shows, and why it matters
Rather than simply asking “can we in principle reconstruct the quantum state from scattering data?”, we now ask “what does the space of possible reconstructions look like?”
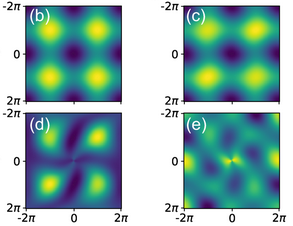
Specifically, we consider how far two different quantum states (or density matrices) are from each other in terms of their scattering signatures (specifically the static structure factor) and also in terms of the overlap of the states themselves. We find a roughly linear relationship between the mean-square distance of the structure factors and the corresponding state overlap (i.e. how “close” the states are) in a range of models and numerical tests. This suggests that the inversion problem (from scattering data → quantum state) is not wildly chaotic or pathological: the “fitness landscape” is reasonably well-behaved, with solutions close in scattering space also close in the state space. We also extend the discussion beyond zero-temperature pure ground states: we provide evidence that thermal equilibrium states, applied magnetic fields, and finite magnetic clusters can be treated in a similar framework.
Why is this significant? For the broader field of quantum materials and quantum many-body physics, it means that scattering experiments
(specifically neutron scattering) could become a more powerful tomographic tool: instead of just measuring correlators or excitations,
one can begin to imagine reconstructing the quantum many-body state (or at least a close approximation) from scattering data.
That opens new routes for materials whose quantum states are of interest for quantum information, many-body entanglement, or unusual phases.
How this builds on our earlier work
In the earlier work, PQM member Jorge Quintanilla proved two theorems for very general Heisenberg-type models:
- that if two models have identical correlators then they must share the same ground state;
- that a candidate N-qubit wave-function cannot reproduce the correlators of a given system unless it is a true ground state of that system.
That theoretical foundation told us that, under favourable conditions, neutron scattering does encode unique information about the ground state.
The new paper takes the next step: given that in principle the ground state is encoded, what is the practical “landscape” of state fitting?
Are there many nearly-equivalent states that give the same scattering signature (making inversion hopeless)?
Or is the mapping reasonably stable (making inversion feasible)?
Our positive findings raise confidence in the viability of state-reconstruction from scattering.
Wider implications and outlook
From a wider perspective in quantum materials and quantum information, the ability to reconstruct or approximate the many-body quantum state of a material from experimentally accessible probes is a big deal.
It means:
- We move from measuring properties (structure factors, excitations, correlators) to inferring states.
- For materials with strong quantum fluctuations, entanglement, or emergent excitations (spin liquids, quantum magnets, etc.), this improves our ability to link experiment and theory.
- For the quantum-technology agenda (materials for qubits, topological phases, etc.) we begin to open a path where the “hardware” quantum state is not opaque but can be characterised more richly.
Of course there are caveats: the mapping is better behaved under certain assumptions (ground state, certain classes of Hamiltonians, scattering of static correlators). Real experiments have noise, finite temperature, instrument resolution, and many complications. Recognising this, one of the key messages of our work is that even when complications enter (thermal states, applied fields, finite clusters) the fitness-landscape approach is still encouraging.
Looking ahead, the natural next steps for our group include:
- Applying the framework to real neutron-scattering data from quantum magnetic materials, and seeing how the tomography approach performs in practice.
- Extending the inversion methodology to dynamic scattering (time- or energy-dependent), which carries even richer information.
- Exploring how this can interface with quantum-simulation or quantum-computing tools (for instance representing candidate states by neural networks or quantum circuits, and fitting to scattering data directly).
Summary
In short: our new paper shows that the dream of “seeing the quantum state” of a material via neutron scattering is moving from abstract possibility towards practical viability. Building on our earlier theoretical theorems, we show that the fitness landscape from scattering data to quantum state is reasonably well-behaved, giving hope that state-reconstruction is feasible. This opens a promising direction for the PQM Group at Kent: combining sophisticated theoretical frameworks with cutting-edge experimental probes to deepen our access to quantum many-body states in materials.
We look forward to sharing further results — stay tuned.