Neutron scattering is a workhorse of materials research. When it comes to quantum materials, it may be even more powerful than we thought
Note: A more easily accessible summary of this work can be read here.
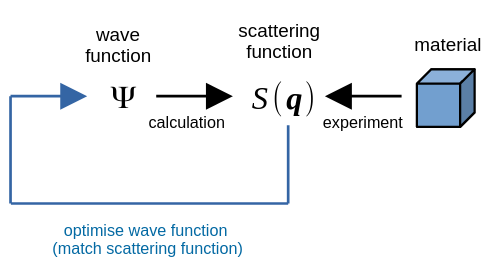
Neutron scattering allows researchers to look inside materials with atomic-scale resolution. Unfortunately, neutron detectors record only momentum and energy, not “phase” – a wave-like property of quantum particles. Thus neutron scattering cannot, usually, determine the state of a material completely. In a paper to appear in Physical Review B (see below), theoretical physicist Jorge Quintanilla of the University of Kent in Canterbury, England, shows that for a broad class of materials of current interest to scientists and engineers this limitation is not present.
Quintanilla considered quantum magnets – insulating materials whose atoms behave like qubits in a quantum computer. At the absolute zero of temperature, their properties are determined by their quantum-mechanical wave function. He asked if a different wave function could lead to the observed neutron scattering pattern. The answer is no, meaning that the wave function is implicitly determined by the neutron scattering measurement.
This result suggests new ways to gain detailed information about the inner workings of quantum magnets and uncovers new connections between quantum materials and quantum information.
Article information:
Quintanilla, J. (2022) “Relationship between the wave function of a magnet and its static structure factor”, Phys. Rev. B 106, 104435 (2022). doi: 10.1103/PhysRevB.106.104435. (or you can download the author’s accepted manuscript for free from the Kent Academic Repository)
Abstract:
We state and prove two theorems about the ground state of magnetic systems described by very general Heisenberg-type models and discuss their implications for magnetic neutron scattering. The first theorem states that two models cannot have the same correlator without sharing the corresponding ground states. According to the second theorem, an N-qubit wave function cannot reproduce the correlators of a given system unless it represents a true ground state of that system. We discuss the implications for neutron scattering inverse problems. We argue that the first theorem provides a framework to understand neutron-based Hamiltonian learning. Furthermore, we propose a variational approach to quantum magnets based on the second theorem where a representation of the wave function (held, for instance, in a neural network or in the qubit register of a quantum processor) is optimised to fit experimental neutron-scattering data directly, without the involvement of a model Hamiltonian.