In a Letter recently published in Physical Review B we describe a novel mechanism for time-reversal symmetry breaking in non-symmorphic superconductors. Here one of the authors gives an accessible account of this work and reflects on its wider significance.
In a Letter recently published in Physical Review B [1] we describe a novel mechanism for time-reversal symmetry breaking in non-symmorphic superconductors. Here I give an accessible summary of that work and offer some reflections on its wider significance for our understanding of magnetism in superconductors.
Sneaky triplet
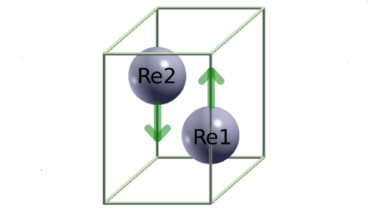
We came upon the new insight while trying to understand the apparent breaking of time-reversal symmetry in the superconducting state of Rhenium. This is an elemental superconductor so understanding time-reversal symmetry breaking in this system is challenging. We used a Density Functional Theory theory that fully took into account all details of the electronic structure and magnetic response of this system, as well as relativistic effects. We then added a phenomenological BCS-type pairing term whose strength was fixed by the requirement that the calculation yields the right critical temperature. Everything else was calculated ab initio.
To our surprise, the theory yields not just singlet pairing, as predicted by BCS, but also an additional, triplet pairing component. This additional component is similar to the one induced by spin-orbit coupling in otherwise conventional, but non-centrosymmetric, superconductors (NCS). However the crystal structure of Re does have a centre of inversion, so it seems the induction of subsidiary triplet pairing is not confined to non-centrosymmetric materials, but can also occur in systems with screw axes or glide planes or, more precisely, non-symmorphic superconductors (NSS). Just as the triplet pairing in induced by Rashba spin-orbit coupling has to respect all the symmetries of the crystal, this new type of spin orbit coupling induced triplet pairing existing in NSS does not break any additional symmetries either – just gauge symmetry. However, it existence teaches us that the interaction potential we put in at the start of our calculation was not general enough – an additional triplet-pairing term can be added without affecting the symmetry of the problem.
Weird magnetism
The biggest surprise came when we added the new term to our theory. We then found that there was a coupling between superconductivity and magnetism and that the ground state broke time-reversal symmetry – in other words, the superconducting ground state was magnetic. However, this was no ordinary magnetic state: the magnetic moments within the unit cell were arranged in such a way as to lead to zero net magnetisation, like in an anti-ferromagnet. Unlike the case of an anti-ferromagnet, though, the magnetic texture repeated from unit cell to unit cell, so this new state respects translational symmetry.
The new, broken time-reversal symmetry state only emerges when the new adjustable parameter (the strength of the pairing interaction in the triplet channel) is large enough. Moreover, depending on the size of this parameter there may be two, consecutive superconducting phase transitions (with the magnetism appearing only at the lower critical temperature) or there may be a single, superconducting transition straight into the anomalous superconducting state with broken time-reversal symmetry. Interestingly, the theory gives an excellent fit to the available data on the temperature-dependence of the specific heat of Re for values placing this substance firmly in the regime where there is a single transition into the state with broken time-reversal symmetry (other values lead to much poorer fits). This fixes the second parameter in the theory, allowing us to make parameter-free predictions including an unusual, spin-split density of states whose observation would provide an unequivocal proof of this new, exotic state of matter.
Computational experiments
Given the surprising nature of this new state it was important to understand its mechanism, and whether it could be applicable to other materials as well. We did this through a couple of computer experiments.The experiments exploited the flexibility of our simulations to force the system into crystal structures that would not be energetically stable and see how the electronic state changes under such large perturbation, yielding insights into the underlying mechanisms.
In the first experiment we artificially modified the crystal structure by gradually removing the screw axis. We saw that the magnetic moment diminished, and there was a critical point where it disappeared completely. This confirmed that the time-reversal symmetry breaking was linked to the non-symmorphic crystal structure.
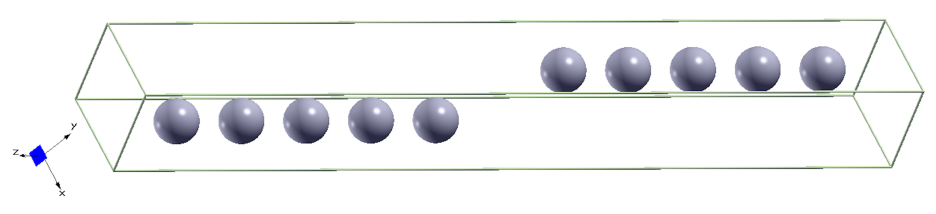
Given the similarities between the triplet component induced by spin-orbit coupling in NCS and this new type of triplet pairing discovered in NSS it was interesting to enquire whether we could use what we know about NCS to gain a better understanding of the mechanism of the broken time-reversal symmetry in NSS. Indeed, although the Rashba-induced triplet pairing component in NCS does not break time-reversal symmetry it is known that a magnetisation can emerge at the interface between twin domains of a NCS [2]. This was the subject of our second computer experiment: we enlarged the unit cell, making many copies of the first Re atom followed by many copies of the second Re atom (see image, above). Such structure is actually identical to a twin boundary between two NCS superconductors: one occupying the first half of the enlarged unit cell, the other occupying the second half. We saw indeed that the magnetic moment was not equal in strength on all the Re atoms, but was largest at the edges of the cell and in the middle – precisely the boundaries between the twin domains.
A generic mechanism
Our computer experiments produced a satisfyingly unified view not only of triplet pairing but also of broken time-reversal symmetry in NCS and NSS. They suggest that broken time-reversal symmetry through magnetic textures like the one we uncovered in Re may occur in many other NSS. The case for broken time-reversal symmetry in Re itself needs to be built from more experimental data but I am quite confident that the mechanism of broken time-reversal symmetry we have identified will be in operation in many NSS.
Glossary
Non-centrosymmetric superconductors (NCS)
Superconducting materials whose crystal structure lacks a centre of inversion. A centre of inversion is a point in space such that, given any atom belonging to the crystal structure under consideration, a line going from that atom to that point and prolonged an equal distance beyond that point finds an identical atom at its end. In non-centrosymmetric there is no such special point cannot be found.
Non-symmorphic superconductors (NSS)
Superconducting materials whose crystal structure has symmetries that do not involve translating all the atoms in the system by a fixed amount but do not leave any point in space unchanged. A symmetry of a crystal lattice is a spatial transformation that, if applied to all points in space, leaves the crystal unchanged. Crystals are periodic, which means that they repeat in space in a regular fashion and therefore always have translational symmetry: if you displace the crystal in certain direction by a certain amount, every atom lands on the previous position of an identical atom, and the crystal remains unchanged. Translations change every point in space to a new location. An example of a spatial operation that leaves some points in space where they are would be a mirror symmetry. In a crystal structure with mirror symmetry, there is a plane such that all atoms in the system have a “mirror twin” on the other side of the plane, at an equal distance to it. This particular transformation leaves all the points on the mirror plane itself unchanged – so atoms sitting on that plane do not need to have a twin. Other examples of symmetries that leave some points unchanged include rotation symmetries (for instance, a snowflake has 6-fold rotational symmetry around its central point, which remains unchanged) and inversion symmetry (the special symmetry posssessed by crystals with a centre of inversion, see the explanation of non-centrosymmetric systems, above). In non-symmorphic systems there are some symmetries that change all the points in space but are not simple translations. An example of this would be a screw axis. A crystal has a screw axis if there exists a line such that if we rotate all the atoms in the crystal around that line by the same amount and displace them by the same distance parallel to that line every atom ends up at the location of an identical one.
References
[1] G. Csire, J. F. Annett, J. Quintanilla and B. Újfalussy, “Magnetically textured superconductivity in elemental rhenium“, Physical Review B 106, L020501 (2022). (doi:10.1103/PhysRevB.106.L020501) (KAR id:81194) (arXiv:2005.05702)
[2] E. Arahata, T. Neupert, and M. Sigrist, “Spin currents and spontaneous magnetization at twin boundaries of noncentrosymmetric superconductors”, Physical Review B 87, 220504(R) (2013). (doi: 10.1103/PhysRevB.87.220504)